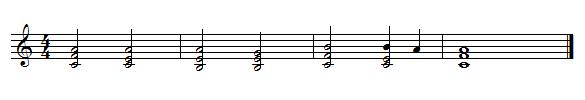
The common-practice notation we all know and love is an example of what I call a "diatonic notation". See Carl's 1st Law of Notation for the distinction.
Here, I'll give an example of octatonic notations at work. These are quick and dirty examples only.
First, have a look at this:
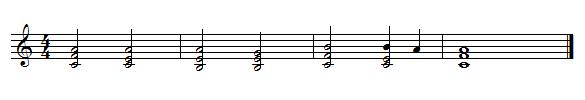
This may look like ordinary notation, but it's not! For here, every step over a line or space is one step through an 8-tone scale, rather than one step through the 7-tone diatonic scale as usual.
Let's tune this in the scale known as hanson[8], using nominals A-H. The scale step pattern 1-4-6 gives the following triads...
C F H ~ 4:5:6 [1M]
D G A ~ 15:21:25 [2s]
E H B ~ 4:5:6 [3M]
F A C ~ 5:7:8 [4S]
G B D ~ 28:35:40 [5%]
H C E ~ 15:20:24 [6m]
A D F ~ 35:42:60 [7%]
B E G ~ 15:20:24 [8m]
Given this scheme, the above notation represents the following chord progression:
H-----H-----H.....G.....A-----A...H---H
F.....E-----E-----E.....F.....E----...F
C-----C.....B-----B.....C-----C-------C
1M____6m____3M____8m____4S__sus6__6m__1M
Here's what it sounds like: KleismicExample.mid
We can use accidentals to extend the notation beyond 8 notes. Because the scale is non-MOS there are three possible accidental pairs...
# and b show 648:625 (4 generators, about 63 cents)
^ and v show 419904:390625 (8 generators, about 126 cents)
+ and - show 78125:69984 (7 generators, about 190 cents)
Finally, just for fun, here's what the notation at the top sounds like when tuned to harmonics 8-16 instead of hanson[8].